|
Přípravné
příklady k maturitní zkoušce Přiklady, které se objevily
v maturitních testech autor všech úloh: CERMAT |
||
|
2.
Algebraické výrazy |
||
1)
Vytkněte a rozložte na součin: (vzorové příklady)
![]()
2)
Proveďte: (vzorové příklady)
![]()
3)
Proveďte: (vzorové příklady)
a)
![]()
b)
![]()
c)
![]()
![]()
4)
Pro ![]() je dán výraz: (vzorové příklady)
je dán výraz: (vzorové příklady)
![]()
a)
Vypočtěte hodnotu
výrazu pro ![]() .
.
b)
Vypočtěte, pro kterou
hodnotu proměnné x je výraz roven nule.
5)
Pro ![]() určete podmínky, pro něž má smysl výraz: (vzorové příklady)
určete podmínky, pro něž má smysl výraz: (vzorové příklady)
![]()
6)
Pro ![]() a
a ![]() proveďte a upravte na co nejjednodušší tvar: (vzorové příklady)
proveďte a upravte na co nejjednodušší tvar: (vzorové příklady)
![]()
7)
Pro ![]() zjednodušte: (vzorové příklady)
zjednodušte: (vzorové příklady)
![]()
8)
Pro ![]() proveďte: (vzorové příklady)
proveďte: (vzorové příklady)
![]()
9)
Pro ![]() proveďte a zjednodušte: (vzorové příklady)
proveďte a zjednodušte: (vzorové příklady)
![]()
10) Pro
![]() zjednodušte: (vzorové příklady)
zjednodušte: (vzorové příklady)
![]()
11) Vyjádřete
jako jedinou mocninu se základem 2: (vzorové příklady)
![]()
12) Pro
![]() zjednodušte: (vzorové příklady)
zjednodušte: (vzorové příklady)
![]()
13) Jsou
dány dva výrazy: ![]() s proměnnou
s proměnnou ![]()
Rozhodněte o každém z následujících tvrzení, zda je
pravdivé či nikoli.
-
Pro x = -1 má první z obou
výrazů smysl
-
Pro x = 1
má druhý z obou výrazů smysl
-
Společný jmenovatel obou výrazů může být x2
+ x
-
Pro kladné hodnoty proměnné x je
součet obou výrazů roven ![]() .
.
14) Za
jakých podmínek pro ![]() mý výraz
mý výraz ![]() smysl? (vzorové příklady)
smysl? (vzorové příklady)
a)
c ≠ ±2
b)
c ≠ 0; c ≠ ±2
c)
c ≠ 0;c ≠ 2
d)
c ≠ 0;c ≠ -2
e)
za jiných podmínek
15) Jaká
je hodnota výrazu ![]() pro
pro
![]() ? (vzorové příklady)
? (vzorové příklady)
a)
![]()
b)
![]()
c)
![]() 2
2
d)
![]() 2,2
2,2
e)
![]() 3
3
16) Pro
které reálné hodnoty proměnné x není definován výraz ![]() ? (vzorové příklady)
? (vzorové příklady)
a)
pro x = 0
b)
pro x = 1 a pro x = -2
c)
pro x = -1 a pro x = 2
d)
pro jiné dvě hodnoty
e)
výraz je definován pro všechna reálná
čísla
17) Pro
![]() upravte: (jaro 2012)
upravte: (jaro 2012)
![]()
18) Přiřaďte
k výrazům jejich adekvátní vyjádření: (jaro 2012)
-
![]()
-
![]()
-
![]()
a)
![]()
b)
![]()
c)
![]()
d)
![]()
e)
žádné z uvedených
19) Pro
![]() proveďte: (jaro 2013)
proveďte: (jaro 2013)
![]()
20) Pro
![]() upravte výraz a uveďte podmínky. (jaro 2013)
upravte výraz a uveďte podmínky. (jaro 2013)
Uveďte celý postup řešení.
![]()
21) Pro
![]() rozložte na součin dvojčlenů: (podzim 2013)
rozložte na součin dvojčlenů: (podzim 2013)
![]()
22) Pro
![]() zjednodušte:
(podzim 2013)
zjednodušte:
(podzim 2013)
Uveďte
celý postup řešení.
![]()
23) Pro
![]() proveďte: (vzorový test 2013)
proveďte: (vzorový test 2013)
![]()
24) Pro
![]() zjednodušte výraz a uveďte podmínky.
(vzorový test 2013)
zjednodušte výraz a uveďte podmínky.
(vzorový test 2013)
Uveďte
celý postup řešení.
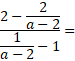
25) Rozšířením lomeného výrazu ![]() , kde
, kde ![]() , dostáváme
, dostáváme ![]() .
.
Zapište výraz, kterým nahradíte
v čitateli symbol ¤. (vzorový test 2013)
26) Vypočtěte
jednu třetinu z ![]() , kde
, kde ![]() . (jaro 2014)
. (jaro 2014)
27) Výraz (s
proměnnou ![]() ) zjednodušte
tak, aby neobsahoval závorky. (jaro 2014)
) zjednodušte
tak, aby neobsahoval závorky. (jaro 2014)
![]()
28) Pro
![]() zjednodušte: (jaro 2014)
zjednodušte: (jaro 2014)
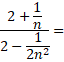
Uveďte
celý postup řešení.
29) Výraz
s proměnnou ![]() rozložte na součin. (podzim 2014)
rozložte na součin. (podzim 2014)
![]()
30) Pro
![]() upravte výraz: (podzim 2014)
upravte výraz: (podzim 2014)
![]()
Uveďte
celý postup řešení.
31) Rozhodněte
o každém z následujících tvrzení, zda je pro všechny hodnoty ![]() pravdivé, či nikoli. (podzim 2014)
pravdivé, či nikoli. (podzim 2014)
-
![]()
-
![]()
-
![]()
-
![]()
32) Tiskárna
vytiskne k listů za n sekund. ![]()
Vyjádřete
v závislosti na veličinách k a
n počet listů, které
tiskárna vytiskne za 5 minut. (jaro 2015)
33) Pro ![]() zjednodušte:
(jaro 2015)
zjednodušte:
(jaro 2015)
![]()
Uveďte celý postup řešení.
34) Pro
![]() je dán lomený výraz:
je dán lomený výraz:
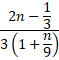
Lomený výraz rozšiřte
číslem 3 a odstraňte závorky. (jaro 2015)
35) Pro
![]() platí:
platí:
![]()
![]()
Který
z následujících výrazů pro ![]() je ekvivalentní s výrazem
je ekvivalentní s výrazem ![]() ?
(jaro 2015)
?
(jaro 2015)
a)
![]()
b)
![]()
c)
![]()
d)
![]()
e)
žádný z uvedených
36) Pro
![]() zjednodušte: (podzim 2015)
zjednodušte: (podzim 2015)
![]()
37) Pro
![]() proveďte umocnění a upravte: (podzim 2015)
proveďte umocnění a upravte: (podzim 2015)
![]()
38) Pro
![]() výraz zjednodušte a uveďte podmínky, pro něž
má výraz smysl. (podzim
2015)
výraz zjednodušte a uveďte podmínky, pro něž
má výraz smysl. (podzim
2015)
![]()
Uveďte celý postup řešení.
39) Určete
všechny hodnoty ![]() , pro které má smysl výraz: (vzorový test 2015)
, pro které má smysl výraz: (vzorový test 2015)
![]()
40) Pro
![]() zjednodušte na tvar bez odmocniny: (vzorový test 2015)
zjednodušte na tvar bez odmocniny: (vzorový test 2015)
a) ![]()
b) ![]()
41) Pro
![]() upravte výraz: (vzorový test 2015)
upravte výraz: (vzorový test 2015)
![]()
Uveďte celý postup řešení.
42) Nádrž
se plní několika stejně výkonnými čerpadly. Dvě čerpadla by prázdnou nádrž
naplnila za x hodin (x > 0).
Vyjádřete
v hodinách, za jak dlouho by prázdnou nádrž naplnilo n
čerpadel ![]() .
(jaro 2016)
.
(jaro 2016)
43) Pro
![]() zjednodušte:
(jaro 2016)
zjednodušte:
(jaro 2016)
![]()
44) Pro
![]() zjednodušte: (jaro 2016)
zjednodušte: (jaro 2016)
![]()
Uveďte celý postup řešení.
45) Zjednodušte: (podzim
2016)
![]()
46) Je
dán výraz:
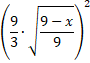
a)
Uveďte všechny hodnoty ![]() ,
pro něž má výraz smysl (podmínky).
,
pro něž má výraz smysl (podmínky).
b)
Výraz zjednodušte do tvaru
dvojčlenu. (podzim
2016)
47) Pro
![]() zjednodušte: (podzim
2016)
zjednodušte: (podzim
2016)
![]()
Uveďte celý postup řešení.
48) Všechny
vagóny nákladního vlaku jsou plně naloženy pískem, který přivezla malá a velká
nákladní auta. Malých aut bylo n (n je číslo sudé), velkých aut
bylo o polovinu více než malých aut. Písek z malého auta naplní osminu
vagónu a písek z velkého auta čtvrtinu vagónu.
V závislosti na
veličině n vyjádřete počet vagónů
nákladního vlaku. (podzim
2016)
Výraz zapište
ve tvaru jednočlenu.
49) Je
dán výraz:
![]()
Určete množinu všech ![]() ,
pro která má výraz hodnotu 0. (jaro 2017)
,
pro která má výraz hodnotu 0. (jaro 2017)
50) Pro
![]() zjednodušte výraz: (jaro 2017)
zjednodušte výraz: (jaro 2017)
![]()
51) Pro ![]() zjednodušte: (jaro 2017)
zjednodušte: (jaro 2017)
![]()
Uveďte celý postup řešení.
52) Vyjádřete
jednu polovinu rozdílu výrazů ![]() a
a ![]() v uvedeném pořadí v co
nejjednodušším tvaru
v uvedeném pořadí v co
nejjednodušším tvaru ![]() .
(podzim 2017)
.
(podzim 2017)
53) Pro
![]() zjednodušte: (podzim 2017)
zjednodušte: (podzim 2017)
![]()
54) Pro
![]() zjednodušte: (podzim 2017)
zjednodušte: (podzim 2017)
![]()
Uveďte celý postup řešení.
55) Eva,
její starší kamarád Marek a jeho vlastní babička dnes mají narozeniny. Babičce
je 72 let, Markovi je m let a Evě je o d let méně než babičce.
Rozhodněte o každém
z následujících tvrzení, zda je pravdivé, či nikoli. (podzim 2017)
-
Všem osobám je dohromady (144 + m – d) let.
-
Babička je (72 :
m)krát starší než Marek.
-
Eva je o (72 + d – m)
let mladší než Marek.
-
Když se narodila Eva, Markovi bylo (m + d – 72) let.
56) Odstraňte závorky a zjednodušte ![]() : (jaro
2018)
: (jaro
2018)
![]()
57) Pro
![]() zjednodušte: (jaro
2018)
zjednodušte: (jaro
2018)
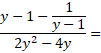
Uveďte celý postup řešení.
58) Rozhodněte o každém z následujících
tvrzení, je-li pravdivé pro všechna ![]() ,
či nikoli. (jaro
2018)
,
či nikoli. (jaro
2018)
-
![]()
-
![]()
-
![]()
-
![]()
59) Je
dán výraz:
![]()
Určete
všechny hodnoty ![]() , pro které je hodnota výrazu rovna nule.
(podzim
2018)
, pro které je hodnota výrazu rovna nule.
(podzim
2018)
60) Pro
![]() je dán výraz:
je dán výraz:
![]()
-
Výraz
zjednodušte.
-
Určete,
pro která reálná čísla a má výraz smysl (tj. podmínky). (podzim
2018)
Uveďte celý postup
řešení.
61) Vlak
má tři vagony, všechny se stejným počtem míst. V každém vagonu je o 20
míst k stání více než k sezení.
Při odjezdu z Roztok by vlak zaplněn
přesně do poloviny své kapacity.
V prvním a posledním vagonu byla
všechna místa k sezení obsazená, ale ve druhém vagonu zůstalo 25% míst k sezení volných.
(Kapacita vlaku je součet počtu všech míst
k stání a sezení. Každý cestující obsadil buď jedno místo k stání,
nebo jedno místo k sezení.)
Počet míst k sezení
v jednom vagonu označme n.
Vyjádřete
v závislosti na veličině n
počet všech cestujících, kteří při odjezdu z Rostok
(jaro 2019)
-
byli ve vlaku
-
ve vlaku stáli
62) Pro
![]() zjednodušte: (jaro 2019)
zjednodušte: (jaro 2019)
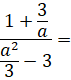
63) Je
dán výraz ![]() s reálnou proměnnou a.
s reálnou proměnnou a.
Které tvrzení je
pravdivé? (jaro 2019)
a)
Pro ![]() je výraz kladný.
je výraz kladný.
b)
Pro ![]() je hodnota výrazu 0.
je hodnota výrazu 0.
c)
Hodnota výrazu nemůže být nikdy nulová.
d)
Pro všechna ![]() je výraz roven
je výraz roven ![]()
e)
Pro některá a je výraz roven ![]() .
.
64) Pro
![]() upravte na co nejjednodušší tvar
(výsledný výraz nesmí obsahovat závorky): (podzim 2019)
upravte na co nejjednodušší tvar
(výsledný výraz nesmí obsahovat závorky): (podzim 2019)
![]()
Uveďte celý postup řešení.
65) Dva
mniši opisovali rukopisy. Každý z nich pracoval stále stejným tempem. Mladší
Dominik opsal za každý týden n stránek rukopisu ![]() .
Starší Alfons byl pomalejší a každý týden opsal o třetinu méně stránek než
Dominik. (podzim 2019)
.
Starší Alfons byl pomalejší a každý týden opsal o třetinu méně stránek než
Dominik. (podzim 2019)
-
Určete v závislosti na n, kolik
stránek celkem opsali oba mniši za 3 týdny.
-
Určete, za kolik týdnů opsali oba mniši
celkem 100n stránek rukopisu.
66) Pro
![]() upravte do tvaru trojčlenu: (jaro 2020)
upravte do tvaru trojčlenu: (jaro 2020)
![]()
67) Pro
všechny kladné reálné hodnoty veličin a, b, c platí:
![]()
![]()
Vyjádřete co
nejjednodušším způsobem veličinu b
pouze v závislosti na veličině c.
(jaro 2020)
68) Pro
![]() zjednodušte: (jaro 2020)
zjednodušte: (jaro 2020)
![]()
Uveďte celý postup řešení.
69) ![]()
Uvedená rovnost výrazů
platí (jaro 2020)
a)
pro všechna reálná čísla x a y.
b)
pro libovolné reálné číslo y a
každé nenulové reálné číslo x
c)
jen pro y = x, přičemž x je
libovolné reálné číslo
d)
jen pro y = x, přičemž x je
libovolné nenulové reálné číslo
e)
pro všechna reálná čísla x a y,
kde ![]() a současně
a současně ![]() .
.
70) Pro
![]() zjednodušte: (podzim 2020)
zjednodušte: (podzim 2020)
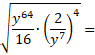
71) Určete
všechny hodnoty ![]() ,
pro které má smysl výraz: (podzim 2020)
,
pro které má smysl výraz: (podzim 2020)
![]()
72) Pro
![]() zjednodušte (podzim 2020)
zjednodušte (podzim 2020)
(výsledný výraz nesmí obsahovat závorky):
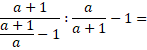
Uveďte celý postup řešení.
73) Je
dán výraz:
![]()
Který z následujících
výrazů je pro každé ![]() ekvivalentní s daným výrazem? (podzim 2020)
ekvivalentní s daným výrazem? (podzim 2020)
a)
25
b)
12,5
c)
0,2a
d)
0,5a25
e)
Žádný z uvedených výrazů není
s daným výrazem ekvivalentní.
74) Pro
![]() upravte výraz a vyjádřete jej ve tvaru
odmocniny o základu a. (jaro 2021)
upravte výraz a vyjádřete jej ve tvaru
odmocniny o základu a. (jaro 2021)
![]()
75) Pro
![]() zjednodušte: (jaro 2021)
zjednodušte: (jaro 2021)
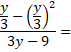
Uveďte celý postup řešení.
76) Je
dán výraz:
![]()
Hodnota výrazu
![]() je rovna nule pro (jaro 2021)
je rovna nule pro (jaro 2021)
a) alespoň
tři celá čísla
b) právě
dvě záporná celá čísla
c) právě
jedno kladné a jedno záporné celé číslo
d) právě
dvě kladná celá čísla
e) právě
jedno celé číslo
77) Pro ![]() odstraňte závorky a sečtěte. (jaro
2021 – mimořádný termín)
odstraňte závorky a sečtěte. (jaro
2021 – mimořádný termín)
Výsledný výraz vyjádřete jediným členem,
a to bez závorek.
![]()
78) Jedna
strana obdélníku je o pětinu kratší než strana čtverce a obsahy obou těchto
útvarů jsou stejné. Délku strany čtverce označíme 𝑎.
Vyjádřete
délku delší strany obdélníku v závislosti na veličině 𝑎.
(jaro
2021 – mimořádný termín)
79) Pro ![]() zjednodušte:
(jaro
2021 – mimořádný termín)
zjednodušte:
(jaro
2021 – mimořádný termín)
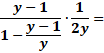
Uveďte celý postup řešení.
80) Je
dán výraz V s reálnou
proměnnou x:
![]()
Které
z tvrzení je pravdivé? (jaro
2021 – mimořádný termín)
a)
Hodnota výrazu V je nulová pro ![]() .
.
b)
Hodnota výrazu V je rovna 2 pro ![]()
c)
Hodnota výrazu V je pro ![]() menší než pro
menší než pro ![]()
d)
Hodnota výrazu V nemůže být rovna 1.
e)
Hodnota výrazu V nemůže být nikdy záporná.
81) Je
dán výraz:
![]()
Určete
![]() ,
pro které je hodnota daného výrazu rovna nule. (podzim 2021)
,
pro které je hodnota daného výrazu rovna nule. (podzim 2021)
82) Pro
![]() zjednodušte: (podzim 2021)
zjednodušte: (podzim 2021)
![]()
Uveďte celý postup řešení.
83) Pro
![]() upravte na mocninu o základu
4. (jaro 2022)
upravte na mocninu o základu
4. (jaro 2022)
![]()
84) Pro
![]() zjednodušte: (jaro 2022)
zjednodušte: (jaro 2022)
![]()
Uveďte celý postup řešení.
85) Určete
množinu všech ![]() ,
pro která má smysl výraz: (podzim 2022)
,
pro která má smysl výraz: (podzim 2022)
![]()
86) V
bedýnce jsou jogurty a rohlíky pro děti z letního tábora.
V bedýnce je 𝑥 jogurtů a 𝑟-krát
více rohlíků než jogurtů.
Jeden jogurt stál 10 korun a jeden rohlík 2
koruny.
Za všechny jogurty a rohlíky, které jsou v
bedýnce, se zaplatilo dohromady 𝑝 korun.
(𝑥, 𝑟, 𝑝
jsou z množiny kladných celých čísel.)
Vyjádřete počet jogurtů 𝑥
v bedýnce v závislosti na veličinách 𝑟 a
𝑝.
(podzim 2022)
87) Pro
![]() zjednodušte: (podzim 2022)
zjednodušte: (podzim 2022)
![]()
Uveďte celý postup řešení.
88) Pro
![]() zjednodušte: (jaro 2023)
zjednodušte: (jaro 2023)
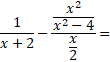
Uveďte celý postup řešení.
ŘEŠENÍ:
|
1) |
|
|
|
2) |
|
|
|
3) |
a) |
|
|
|
b) |
|
|
|
c) |
|
|
4) |
a) |
|
|
|
b) |
|
|
5) |
|
|
|
6) |
|
|
|
7) |
|
|
|
8) |
|
|
|
9) |
|
|
|
10) |
|
|
|
11) |
|
|
|
12) |
|
|
|
13) |
|
-
ne -
ano -
ano -
ano |
|
14) |
|
d |
|
15) |
|
c |
|
16) |
|
e |
|
17) |
|
|
|
18) |
|
-
c -
d -
b |
|
19) |
|
|
|
20) |
|
|
|
21) |
|
|
|
22) |
|
|
|
23) |
|
|
|
24) |
|
|
|
25) |
|
|
|
26) |
|
|
|
27) |
|
|
|
28) |
|
|
|
29) |
|
|
|
30) |
|
|
|
31) |
|
-
ne -
ano -
ano -
ne |
|
32) |
|
|
|
33) |
|
2 |
|
34) |
|
|
|
35) |
|
a |
|
36) |
|
|
|
37) |
|
|
|
38) |
|
|
|
39) |
|
|
|
40) |
a) |
|
|
|
b) |
|
|
41) |
|
|
|
42) |
|
|
|
43) |
|
|
|
44) |
|
|
|
45) |
|
|
|
46) |
a) |
|
|
|
b) |
|
|
47) |
|
|
|
48) |
|
|
|
49) |
|
|
|
50) |
|
|
|
51) |
|
|
|
52) |
|
|
|
53) |
|
|
|
54) |
|
|
|
55) |
|
-
ano -
ano -
ne -
ano |
|
56) |
|
|
|
57) |
|
|
|
58) |
|
-
ano -
ne -
ne -
ano |
|
59) |
|
|
|
60) |
|
-
-
|
|
61) |
|
-
-
|
|
62) |
|
|
|
63) |
|
c |
|
64) |
|
|
|
65) |
|
-
-
za 60 týdnů |
|
66) |
|
|
|
67) |
|
|
|
68) |
|
|
|
69) |
|
d |
|
70) |
|
|
|
71) |
|
|
|
72) |
|
|
|
73) |
|
b |
|
74) |
|
|
|
75) |
|
|
|
76) |
|
b |
|
77) |
|
|
|
78) |
|
|
|
79) |
|
|
|
80) |
|
d |
|
81) |
|
|
|
82) |
|
|
|
83) |
|
|
|
84) |
|
|
|
85) |
|
|
|
86) |
|
|
|
87) |
|
|
|
88) |
|
|