Přípravné příklady ke státní maturitě 5. Posloupnosti a finanční matematika zpět
1)
Uvažujme všechna po sobě jdoucí lichá čísla od 35 do 135 (včetně obou
uvedených čísel.)
a.
Určete
jejich počet
b.
Určete jejich součet. 35 + 37 + … +
135
2)
V geometrické posloupnosti ![]() platí:
platí:
![]()
Jaký je kvocient posloupnosti?
a)
![]()
b)
![]()
c)
2
d)
4
e)
6
3)
V geometrické posloupnosti s kladnými členy platí:
![]()
Do kterého
z uvedených intervalů patří třetí člen a3
poslouposti?
a)
![]()
b)
![]()
c)
![]()
d)
![]()
e)
![]()
4)
Souvislý rovinný obrazec se skládá z několika „domečků“ tvořených
vždy obdélníkem a rovnostranným trojúhelníkem. Šířka prvního obdélníku je 50
cm, každý následující obdélník je o 2 cm užší. Poslední obdélník má šířku 16
cm. Všechny obdélníky mají délku 52 cm.
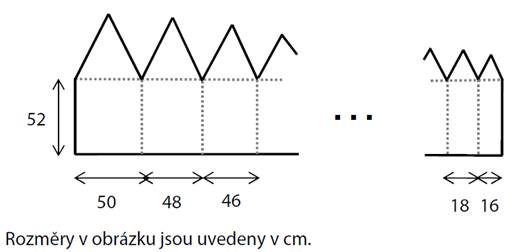
Jaký je obvod celého obrazce?
a)
1 688
cm
b)
1 735
cm
c)
1784
cm
d)
1 886
cm
e)
Jiný
obvod
5)
*Pro
![]() řeště rovnici:
řeště rovnici:
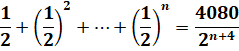
Uveďte celý postup řešení.
6)
*V Kocourkově
vydláždili cestu od radnice kulatými dlaždicemi.

První den položili jednu
dlaždici s průměrem 51 cm, druhý den dvě dlaždice s průměrem 52 cm,
další den tři dlaždice s průměrem 53 cm atd. Až do konce pokračovali podle
stejného pravidla. Každý den položili o 1 dlaždici více než v předešlém
dni a zároveň se průměr dlaždic zvětšil o 1 cm.
Poslední den položili největší
počet dlaždic, a to s průměrem 130 cm.
a)
Vypočtěte,
kolik dlaždic na cestě mělo průměr 130 cm.
b)
Vypočtěte,
kolika dlaždicemi v Kocourkově vydláždili celou cestu.
c)
Vypočtěte
průměr dlaždice, která byla položena na cestě jako tisící v pořadí.
U všech částí úlohy uveďte celý postup řešení.
7)
Kocourkovští postavili plot ze stejně velkých tmavých a světlých krychlí.
Ve spodní řadě plotu umístili tmavé krychle těsně vedle sebe. Na každé druhé
tmavé krychli pak postavili sloupek ze světlých krychlí. Nejnižší je první
sloupek s jednou světlou krychlí. Každý následující sloupek je vždy o jednu
krychli vyšší. Nejvyšší sloupek tvoří n
světlých krychlí. Plot je zakončen tmavou krychlí za nejvyšším sloupkem.
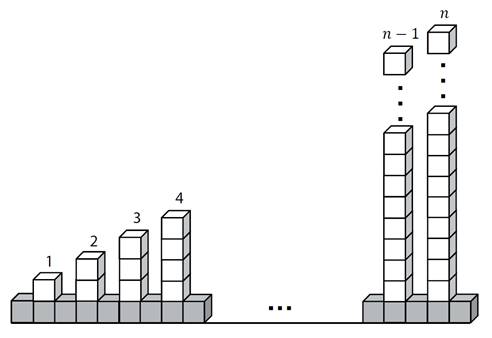
a)
Vyjádřete
počet tmavých krychlí v závislosti na veličině n,
kde ![]()
b)
Určete
počet všech krychlí (tmavých i světlých) použitých na stavbu plotu pro n = 99.
8)
V geometrické posloupnosti platí:
q = -2
a1 + a2 + a3 + a4
+ a5 = 15,4
Do kterého z uvedených intervalů
patří první člen a1 posloupnosti?
a)
![]()
b)
![]()
c)
![]()
d)
![]()
e)
do
žádného z uvedených
9)
V aritmetické posloupnosti platí:
![]()
Jaké je diference
posloupnosti?
a)
12,5
b)
5
c)
-5
d)
-12,5
e)
-25
10)
Fiktivní obrazec je sestaven s podobných rovnoramenných trojúhelníků.
Sousední trojúhelníky mají vždy jeden společný bod a jejich výšky na základnu
leží na téže přímce. Nejmenší trojúhelník má délku základny 2 cm a velikost
výšky na základnu 1 cm. Každý další trojúhelník má uvedené rozměry dvakrát
větší než předchozí trojúhelník.

a)
Obrazec obsahuje 6 trojúhelníků.
Vypočtěte v cm2 obsah největšího
trojúhelníku.
b)
Obrazec obsahuje 18 trojúhelníků.
Vypočtěte v cm
výšku v celého obrazce.
11)
Je dáno pět po
sobě jdoucích členů aritmetické posloupnosti:
4, x, y, z, -8
Která hodnota
vyjadřuje součet x + y + z ?
a)
-2
b)
 -3
-3
c)
-4
d)
-6
e)
žádná z
uvedených
12)
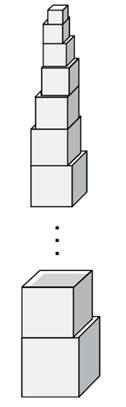
V kocourkově postavili televizní věž se samých krychlí. Dole je
největší krychle s délkou hrany 6 m a každá následující krychle má hranu o
5 cm kratší. Hrana nejmenší krychle měří 3,5 m. Každé dvě sousední krychle mají
jeden společný vrchol. Při pohledu shora žádná z krychlí nepřečnívá přes
níže položenou krychli.
a)
Vypočtěte výšku
televizní věže. (Výsledek
uveďte v metrech a nezaokrouhlujte.)
b)
Vypočtěte v m2
obsah všech nezakrytých vodorovných ploch televizní věže. (Včetně horní stěny nejmenší krychle).
13)
Čtveřice a1, a2, a3, a4
představuje čtyři po sobě jdoucí členy aritmetické posloupnosti. Platí:
a1 = 1, a4 = -8
Čtveřice g1, g2,
g3, g4 představuje čtyři po sobě jdoucí členy geometrické
posloupnosti. Platí: g1 = 1, g4 = -8
Které z následujících tvrzení je nepravdivé?
a)
g1 >
g2
b)
g3
> g4
c)
a2
= g2
d)
a3
= g3
e)
a1
> a2 > a3 > a4
14)
*Do rovnoramenného trojúhelníku ABC je vepsáno nekonečně mnoho čtverců.
Jedna strana každého čtverce leží na základně AB trojúhelníku. Čtverce se
vzájemně dotýkají.
Největší čtverec s délkou strany 20 mm je umístěn
tak, že osa trojúhelníku je současně osou čtverce. Každé dva sousední čtverce
mají jeden společný vrchol a délky stran jsou v poměru 5 : 4.
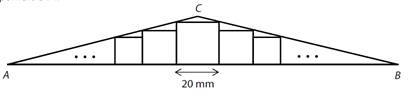
Vypočtěte v mm2 obsah trojúhelníku ABC.
(Uveďte celý postup řešení.)
15)
*Posloupnost obsahuje n
po sobě jdoucích celých čísel a1, a2, …, an,
z nichž nejmenší je a1.
Platí: a1 + a2
+ … + an = n, kde ![]() .
.
a)
Pro
n = 15, vypočítejte a1.
b)
Určete
n, jestliže je a1 = -20.
c)
Vyjádřete
a1
v závislosti ma n a
uveďte množinu všech n, pro
něž daná posloupnost existuje.
Pro všechny
tři části úlohy uveďte postup řešení.
16)
Přiřaďte
ke každé posloupnosti její druhý člen a2.
-
aritmetická posloupnost: ![]()
-
aritmetická posloupnost: ![]()
-
geometrická posloupnost: ![]()
-
geometrická posloupnost: ![]()
