Koule, válec, kužel – příklad 8 - řešení
8. Plášť kužele
rozvinutý do roviny má tvar kruhového výseku se středovým úhlem α = 120° a
obsahem S = 8 482,3 cm2. Vypočítejte rozměry tohoto kužele a
jeho objem.
poloměr kruhového výseku
je vlastně délka boční stěny kužele – s
jelikož ![]() ,
musí platit, že plocha kruhového výseku musí být jednou třetinou obsahu kruhu
se stejným poloměrem – s, tedy:
,
musí platit, že plocha kruhového výseku musí být jednou třetinou obsahu kruhu
se stejným poloměrem – s, tedy:
![]()
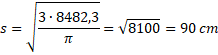
r
– poloměr základny zjistíme tak, že obvod podstavy musí být stejný jako oblouk
kruhového výseku, neboli jedna třetina (120/360) obvodu kruhu s poloměrem S,
tedy:
![]()
![]()
h
– výšku kužele vypočteme z Pythagorovy věty: h2 + r2
= s2
![]()
![]()
boční
stěna - s = 90 cm, poloměr podstavy - r = 30 cm, výška – h = 84,85 cm, objem –
V = 79971,9 cm3