Sinová a kosinová věta – příklady 2
1)
Svisle rostoucí
strom je vysoký 39 m. Místo pozorování P je od paty kmene stromu vzdáleno 101 m
a od vrcholu stromu 128 m. Z místa pozorování P se strom od paty kmenen po
jeho vrchol jeví v zorném úhlu φ.
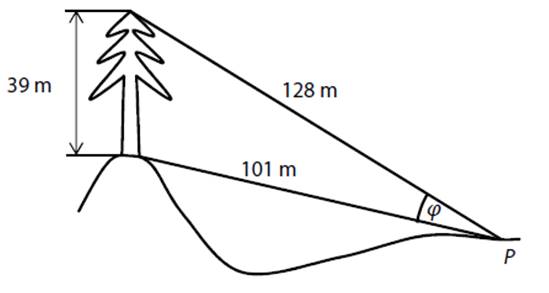
Jaké je velikost
zorného úhlu φ?
(Výsledek
zaokrouhlete na celé stupně, šířku stromu zanedbáváme.)
2)
Na plánu
jsou vyznačeny údaje pořízené při zaměřování vrtné věže V ze dvou
stanovišť A a B.
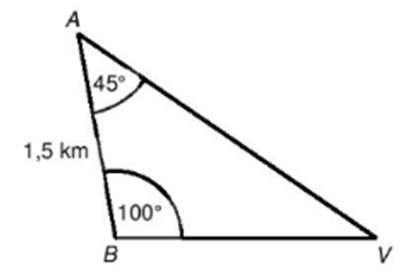
a)
Určete
nejmenší úhel, pod kterým je možné od věže V sledovat současně obě
dstanoviště A a B.
b)
Určete
s přesností na celé metry přímou vzdálenost stanoviště B od vrtné věže V.
3)
Trojúhelník
ABC má délky stran a = 3 cm, b = 5 cm a c = 7 cm. Jaký
je součet velikostí dvou nejmenších vnitřních úhlů trojúhelníku ABC?
4)
Jaká je
délka úhlopříčky AC vypočtená s přesností na desetiny centimetru?
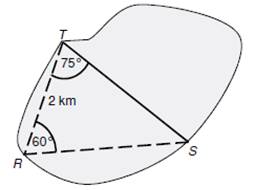
5)
Pozemek
zakreslený v plánku má být rozdělen rovnou hranicí ST na dvě části.
Jaká je délka hranice ST vypočtená s přesností na
desítky metrů?
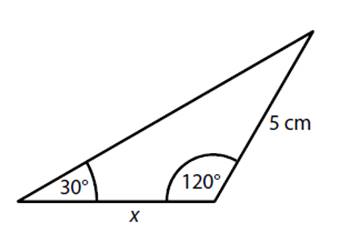
6) Určete délku strany x.
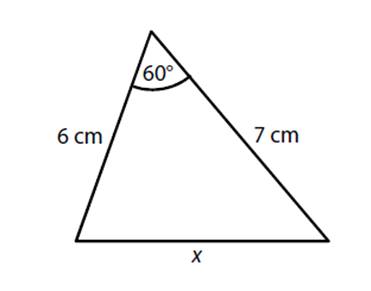
7)
Určete
délku strany x.
8)
Ve čtyřúhelníku ABCD platí:
|AB| = 5 cm, |BC| = 5 cm, |CD| = 6 cm, |BD| = 6 cm, |∡ABD| = 90°
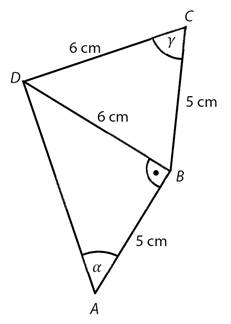
a)
Určete velikost úhlu α = |∡DAB|. Výsledek zaokrouhlete na celé stupně.
b)
Určete velikost úhlu γ = |∡BCD|. Výsledek zaokrouhlete na celé
stupně.
9)
Hranice LP mezi dvěma pozemky má délku 125 metrů. Od
jejího levého okraje L vede rovná pěšina LM, která s touto
hranicí svírá úhel o velikosti 60°.
Na pěšině je stanoviště A, z něhož je hranice LP
vidět pod zorným úhlem 20°.
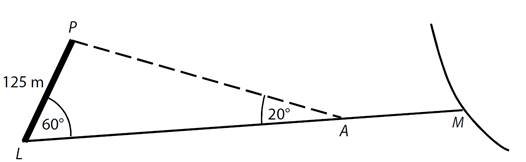
Jaká je vzdálenost AL stanovištěA od levého okraje L hranice LP? Výsledek zaokrouhlete na celé metry.
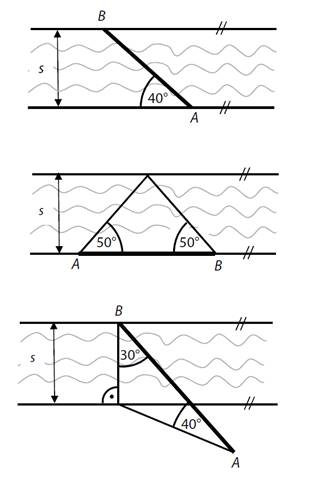
10)
V každé zobrazené situaci je šířka řeky označena symbolem s a
vzdálenost AB je 50 m.
Vypočítejte pro každou situaci odpovídající šířku s řeky. Výsledky
zaokrouhlete na celé metry.
11)
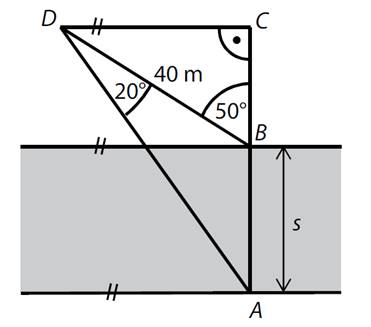
Na břehu řeky se žáci učili obsluhovat měřící přístroje –
teodolit a laserový dálkoměr. Změřili následující údaje:
|BD| = 40
m, |∢ADB| = 20°, |∢CBD| = 50°, |∢ACD| = |∢BCD| = 90°
Jaká je šířka řeky s = |AB|?
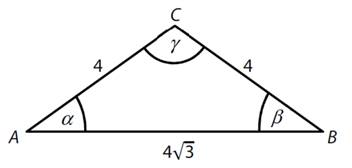
12)
V trojúhelníku
ABC vypočtěte bez zaokrouhlování:
a)
velikost
vnitřního úhlu γ
b)
výšku vc
na stranu AB v centimetrech
(uvedené rozměry jsou uvedené v centimetrech, uveďte celý postup
řešení obou částí úlohy)
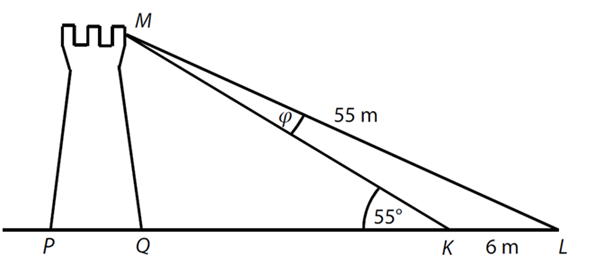
13)
Z místa pozorování M je možné zaměřit body K,
L na obou krajích silnice v zorném úhlu φ.
Platí: |ML| = 55 m, |KL| = 6 m, |∢QKM| = 55°, |∢KML| = φ, body Q, K a L leží
na jedné přímce.
Jaká je velikost zorného úhlu φ? (výsledek
zaokrouhlete na desetiny stupně)
14)
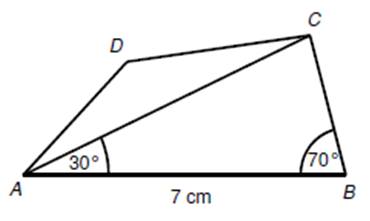
V obdélníku ABCD
o obsahu 28 cm2 je umístěn trojúhelník CDE. Oba obrazce mají
společnou stranu CD.
Platí: |BC| = 4
cm, |CE| = 5 cm, |DE| = 3 cm.
Vypočtěte
velikost úhlu φ.